图的世界 - 在线生成图的工具。

此工具用来生成各种简单图，如完全图、正则图甚至随机图等。你可以选择图的类型、设置顶点数目然后点击“生成”按钮立即得到想要的图。下面还附有 python 源代码供你参考，并给了你一个自定义此工具的机会。

顶点数目图的类型度数边的几率

源码：（修改代码，按 'Alt' + 'R' 运行。）

from processing import *
import math
import random
import document

class CircleLayout(object):
    def __init__(self, g, radius=130):
        self.data = dict()
        for v in g.vertices():
            self.data[v] = (0, 0)
        
        vs = g.vertices()
        theta = math.pi * 2 / len(vs)
        for i, v in enumerate(vs):
            x = radius * math.cos(i * theta)
            y = radius * math.sin(i * theta)
            self.data[v] = (x, y)
            
    def pos(self, v):
        return self.data[v]
        
    def distance_between(self, v1, v2):
        x1, y1 = self.pos(v1)
        x2, y2 = self.pos(v2)
        dx = x1 - x2
        dy = y1 - y2
        return math.sqrt(dx**2 + dy**2)
        
    def shift(self, offsetX, offsetY):
        for v in self.data:
            self.data[v] = (self.data[v][0] + offsetX, self.data[v][1] + offsetY)
            
class Vertex(object):
    """A Vertex is a node in a graph."""

def __init__(self, label=''):
        self.label = label

def __repr__(self):
        """Returns a string representation of this object that can
        be evaluated as a Python expression."""
        return 'Vertex(%s)' % repr(self.label)

__str__ = __repr__
    """The str and repr forms of this object are the same."""

class Edge(object):
    """An Edge is a list of two vertices."""

def __init__(self, *vs):
        """The Edge constructor takes two vertices."""
        if len(vs) != 2:
            raise ValueError, 'Edges must connect exactly two vertices.'
        self.data = tuple(vs)

def __getitem__(self, key):
        return self.data[key]

def __repr__(self):
        """Return a string representation of this object that can
        be evaluated as a Python expression."""
        return 'Edge(%s, %s)' % (repr(self.data[0]), repr(self.data[1]))

__str__ = __repr__
    """The str and repr forms of this object are the same."""

class Graph(object):
    def __init__(self, vs=[], es=[]):
        self.data = dict()
        for v in vs:
            self.add_vertex(v)
            
        for e in es:
            self.add_edge(e)

def add_vertex(self, v):
        """Add a vertex to the graph."""
        self.data[v] = {}

def add_edge(self, e):
        """Adds and edge to the graph by adding an entry in both directions.

If there is already an edge connecting these Vertices, the
        new edge replaces it.
        """
        v, w = (e[0], e[1])
        self.data[v][w] = e
        self.data[w][v] = e

def get_edge(self, *vs):
        if len(vs) != 2:
            raise ValueError, 'Edges must connect exactly two vertices.'

v = vs[0]
        w = vs[1]

try:
            return self.data[v][w]
        except:
            return None

def remove_edge(self, e):
        v, w = (e[0], e[1])
        
        if w in self.data[v]: del self.data[v][w]
        if v in self.data[w]: del self.data[w][v]

def vertices(self):
        return self.data.keys()

def edges(self):
        edges = []
        for v in self.vertices():
            for w in self.vertices():
                edge = self.get_edge(v, w)
                if(edge != None):
                    edges.append(edge)

return edges

def out_vertices(self, v):
        return self.data[v].keys()

def out_edges(self, v):
        out_edges = []
        for w in self.out_vertices(v):
            out_edges.append(self.data[v][w])
        return out_edges

def add_all_edges(self):
        for v in self.vertices():
            for w in self.vertices():
                if(v != w and self.get_edge(v, w) == None):
                    self.add_edge(Edge(v, w))

def sorted_vertices_by_degrees(self):
        result = list(self.vertices())
        for i in range(0, len(result) - 1):
            for j in range(i+1, len(result)):
                if len(self.out_edges(result[i])) > len(self.out_edges(result[j])):
                    t = result[i]
                    result[i] = result[j]
                    result[j] = t
                    
        return result

def add_regular_edges(self, degrees):
        countOfVertices = len(self.vertices())
        maxDegreesICanHave = countOfVertices - 1
        if(degrees > maxDegreesICanHave):
            raise ValueError, 'The specified degrees "' + degrees + '" exceeds the max degrees "' + maxDegreesICanHave + '" I can have.'

totalEdgesToBeAdded = countOfVertices * degrees / 2 # Undirected edges
        totalEdgesHaveBeenAdded = 0
        
        for v in self.vertices():
            if(totalEdgesHaveBeenAdded < totalEdgesToBeAdded):
                myDegrees = len(self.out_edges(v))

for w in self.sorted_vertices_by_degrees():
                    if(myDegrees < degrees):
                        if(v != w and len(self.out_edges(w)) < degrees and self.get_edge(v, w) == None):
                            self.add_edge(Edge(v, w))
                            myDegrees = myDegrees + 1
                            totalEdgesHaveBeenAdded = totalEdgesHaveBeenAdded + 1
                    else:
                        break

if(myDegrees < degrees):
                    raise ValueError, 'Strange things happen. I was trying to increase my degrees to "' + str(degrees) + '", but there is no other vertex for me to add edge when my degrees reached "' + str(myDegrees) + '". Current Vertex: "' + str(v) + '"'

else:
                break
    
    def add_random_edges(self, p):
        for v in self.vertices():
            for w in self.vertices():
                if (v != w and self.get_edge(v, w) == None):
                    x = random.random()
                    if (x <= p):
                        self.add_edge(Edge(v, w))
    
    def is_connected(self):
        to_be_marked = []
        to_be_marked.append(self.vertices()[0])
        while len(to_be_marked) > 0:
            current_vertex = to_be_marked.pop(0)
            current_vertex.marked = True
            for w in self.out_vertices(current_vertex):
                if hasattr(w, 'marked') != True:
                    to_be_marked.append(w)
    
        # Now check if there still are any vertices not marked
        for v in self.vertices():
            if hasattr(v, 'marked') != True:
                return False
    
        # All vertices have been marked
        return True
                
def show_graph(g, layout):
    for v in g.vertices():
        v.pos = layout.pos(v)
        
    for v in g.data:
        for e in g.out_edges(v):
            draw_edge(e)
        
    for v in g.data:
        draw_vertex(v)
    
    if g.is_connected():
        print u'这是一个连通图。'
    else:
        print u'这不是一个连通图。'

def draw_vertex(v, r = 20):
    try: 
        color = v.color
    except:
        color = (255, 255, 0)
        
    stroke(color[0], color[1], color[2])
    fill(color[0], color[1], color[2])
    ellipse(v.pos[0], v.pos[1], r, r)
    fill(0)
    text(v.label, v.pos[0], v.pos[1])
    
def draw_edge(e):
    v, w = e
    stroke(255)
    line(v.pos[0], v.pos[1], w.pos[0], w.pos[1])

def setup():
    canvas = document.getElementById('mycanvas')
    canvasWidth = int(canvas.getProperty('clientWidth'))
    canvasHeight = int(canvas.getProperty('clientHeight'))
    size(canvasWidth, canvasHeight)
    background(0)
    noStroke()
    smooth()
    noLoop()

def draw():
    n = int(#NumberOfVertices
        + 10)
    labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
    vs = []
    for c in labels[:n]:
        vs.append(Vertex(c))

g = Graph(vs)

#g.add_edges()

layout = CircleLayout(g)
    canvas = document.getElementById('mycanvas')
    canvasWidth = int(canvas.getProperty('clientWidth'))
    canvasHeight = int(canvas.getProperty('clientHeight'))
    layout.shift(canvasWidth / 2, canvasHeight / 2)
    
    show_graph(g, layout)

run()

何为简单图？

与复杂图相反，简单图是一个无向图，它不含有圈（圈是同时连接到同一顶点的边）并且在任意两个不同的顶点间至多只存在一条边。简单图中的边形成一个单集（而不是复合集）并且任一边都是不重复的顶点对。一个包含 n 个顶点的简单图，它的每个顶点的度数都是小于 n 的（反过来的命题不成立——因为也存在含有 n 个顶点的非简单图，它的每个顶点的度数也小于 n）。
何为正则图？

正则图：正则图是这样的图，它的任一顶点都有同样数目的邻居，也就是说，每个顶点都有相同的度数。一个顶点的度数为 k 的正则图被称作 k 度正则图或者度为 k 的正则图。
何为完全图？

完全图：完全图是含有这种特性的图，它的任一对顶点间都有一条边相连接。

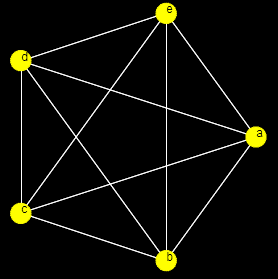一个包含5个顶点的完全图。任一顶点都与每个其他的顶点通过一条边相连接。
证明完全图是正则图。

【证明】

图 G 是完全图，设其共有 n 个顶点。因为它是完全图，所以每两个顶点间都有一条边，也即对于顶点 v_i，共有 (n-1) 个顶点与它相连，也即它的度是 (n-1)。

对于 i = 1, 2, ..., n，degree(v_i) = n - 1. 所以图 G 也是一个度为 (n-1) 的正则图。

【证毕】
何为路径？

图论中，一条路径就是连接着一系列有序顶点的一系列的有序边。一条路径可以是无限的，但是一条有限路径总是有第一个顶点，称为起始点，并且有最后一个顶点。它们都称作是终端顶点。其他的顶点是内部顶点。
何为环？

一个环就是起始顶点与结束顶点相同的一条路径。在环中，起始顶点的挑选是任意的。
何为森林？

森林是不含有环的图（即一个或多个树不交叉的联结）
何为树？

树是不含有环的连通图。
说明：如果每个节点都有到其他节点的路径，那么这个图就是连通的。

在无向图 G 中，两个顶点 u 和 v 被称为是连通的，如果 G 中存在一条从 u 到 v 的路径。否则，它们就被称为是不连通的。如果图中的每对不同的顶点间都是连通的，那么这个图也就被称为是连通的。否则，它被称为是不连通的。

如果每个节点都有到其他节点的路径，那么如果我从图 G 中任选两个顶点 u, v，那么存在一条从 u 到 v 的路径，也就是说 u，v 是连通的。由于 u、v 是任选的，所以图 G 中的两两节点都是连通的，也即图 G 是连通的。

何为简单图？

何为正则图？

何为完全图？

证明完全图是正则图。

何为路径？

何为环？

何为森林？

何为树？

说明：如果每个节点都有到其他节点的路径，那么这个图就是连通的。